Rotate n * n matrix by 90 degrees

This updated information has been further expanded upon on my new website. You can find the updated details here: https://k5kc.com/cs/algorithms/rotate-n-x-n-matrix-by-90-degrees/.

Problem

Rotate the n*n matrix by 90 degrees.

Another way to ask the same problem   

Given an image represented by an NxN matrix, where each pixel in the image is 4 bytes, write a method to rotate the image by 90 degrees. Can you do this in place?

Example

       Example 1                          Example 2
INPUT    >>     OUTPUT      |         INPUT    >>  OUTPUT  
                            |
4                           |             4                                         
                            |
1 2 3 4        1 1 1 1      |     11 12 13 14      41 31 21 11
                            |
1 2 3 4        2 2 2 2      |     21 22 23 24      42 32 22 12
                            |
1 2 3 4        3 3 3 3      |     31 32 33 34      43 33 23 13
                            |
1 2 3 4        4 4 4 4      |     41 42 43 44      44 34 24 14

Solution

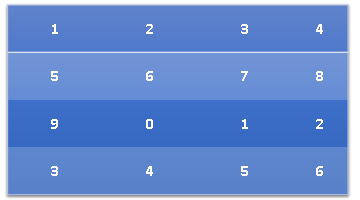
Consider the array

int[,] array = new int[4,4] {
    { 1,2,3,4 },
    { 5,6,7,8 },
    { 9,0,1,2 },
    { 3,4,5,6 }
};

Method 1 - Using 2D array of same size
Here we are

//runner method call
int[,] rotated = RotateMatrix(array, 4);

static int[,] RotateMatrix(int[,] matrix, int n) {
    int[,] ret = new int[n, n];

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            ret[i, j] = matrix[n - j - 1, i];
        }
    }

    return ret;
}

Lets understand this by example.
Consider the array :

Now, when i=0 and j=0, we insert matrix[n-1,0] to ret[0,0]

 Similarily we continue for i=0, and iterating over j.

Now, i=1,  and iterating over j :

Complexity
Time complexity - O(n^2)
Space complexity - O(n^2)

But as we are using lots of space, can we do better?


Method 2 - Without using any extra spaces but O(n^2)
This example is taken from here. Here is the basic algo:

1. Iterate over the 2D array with i and j iterators to the size of N/2
2. Now take the corner elements based on i and j, and swap them accordingly

Java Code

public static void rotate(int[][] matrix) {
    int N = matrix.length;
    for(int i = 0; i < N/2; ++i) {
        for(int j = 0; j < (N+1)/2; ++j) {
            int temp = matrix[i][j];  // save the top element;
            matrix[i][j] = matrix[N-1-j][i];  // right -> top;
            matrix[N-1-j][i] = matrix[N-1-i][N-1-j]; // bottom -> right;
            matrix[N-1-i][N-1-j] = matrix[j][N-1-i];// left -> bottom;
            matrix[j][N-1-i] = temp;                // top -> left;
        }
    }
}

Time complexity - O(n^2)
Space complexity - O(1)

Example
Consider the following matrix with N = 4

i=0,j=0 

Now we see that 1,4,13 and 16 are at the right place. Lets iterate further 
i=0,j=1

Similarly we will go on.
Finally we will get following :

13  9   5   1
14  10  6   2   
15  11  7   3
16  12  8   4

So, to sum up we were doing this:

1           4


13          16

then we rotate the following diamond which is sort of askew

    2
            8
9       
        15

and then the 2nd skewed diamond

        3
5           
            12
    14

so that takes care of the outer edge so essentially we do that one shell at a time until
finally the middle square (or if it's odd just the final element which does not move)

6   7
10  11

so now let's figure out the indices of each layer, assume we always work with the outermost layer, we are doing

[0,0] -> [0,n-1], [0,n-1] -> [n-1,n-1], [n-1,n-1] -> [n-1,0], and [n-1,0] -> [0,0]
[0,1] -> [1,n-1], [1,n-2] -> [n-1,n-2], [n-1,n-2] -> [n-2,0], and [n-2,0] -> [0,1]
[0,2] -> [2,n-2], [2,n-2] -> [n-1,n-3], [n-1,n-3] -> [n-3,0], and [n-3,0] -> [0,2]

so on and so on until we are halfway through the edge
so in general the pattern is

[0,i] -> [i,n-i], [i,n-i] -> [n-1,n-(i+1)], [n-1,n-(i+1)] -> [n-(i+1),0], and [n-(i+1),0] to [0,i]

Can we do better. It may not look obvious, but yes we can. Here is the next solution:

Method 3 - Adding decorator on the top of matrix
This method has been suggested by Drew here. Just keeping it here:

Whilst rotating the data in place might be necessary (perhaps to update the physically stored representation), it becomes simpler and possibly more performant to add a layer of indirection onto the array access, perhaps an interface:

interface IReadableMatrix
{
    int GetValue(int x, int y);
}

If your Matrix already implements this interface, then it can be rotated via a decorator class like this:

class RotatedMatrix : IReadableMatrix
{
    private readonly IReadableMatrix _baseMatrix;

    public RotatedMatrix(IReadableMatrix baseMatrix)
    {
        _baseMatrix = baseMatrix;
    }

    int GetValue(int x, int y)
    {
        // transpose x and y dimensions
        return _baseMatrix(y, x);
    }
}

Rotating +90/-90/180 degrees, flipping horizontally/vertically and scaling can all be achieved in this fashion as well.
Performance would need to be measured in your specific scenario. However the O(n^2) operation has now been replaced with an O(1) call. It's a virtual method call which is slower than direct array access, so it depends upon how frequently the rotated array is used after rotation. If it's used once, then this approach would definitely win. If it's rotated then used in a long-running system for days, then in-place rotation might perform better. It also depends whether you can accept the up-front cost.
As with all performance issues, measure, measure, measure!

Reference

• http://stackoverflow.com/questions/42519/how-do-you-rotate-a-two-dimensional-array