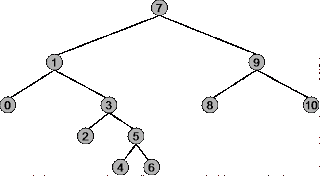
Consider the tree
Inorder traversal prints the binary tree in increasing order in case of Binary Search Tree, but here we are discussing any binary tree.
To traverse a binary tree in Inorder, following operations are
carried-out :
- Traverse the left most subtree starting at the left
external node,
- Visit the root, and
- Traverse the right subtree
starting at the left external node.
Therefore, the Inorder traversal of the above tree will outputs:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Solutions
There are 3 solutions to achieve this. One is iterative and other is
recursive. As we move from recursive to iterative, stack is the obvious
choice. But we also have Morris Traversal.
Method 1 - Recursive solution
inorder(Node *root)
{
if(root)
{
inorder(root->left);
printf("Value : [%d]", root->value);
inorder(root->right);
}
}
Method 2 - Iterative solution using Stack
Using
Stack is the obvious way to traverse tree without recursion. Below is an algorithm for traversing binary tree using stack. See
this for step wise step execution of the algorithm.
1) Create an empty stack S.
2) Initialize current node as root
3) Push the current node to S and set current = current.left until current is NULL
4) If current is NULL and stack is not empty then
a) Pop the top item from stack.
b) Print the popped item, set current = current.right
c) Go to step 3.
5) If current is NULL and stack is empty then we are done.
Here is the code in java:
public static <T> void InorderTraversalIterativeWithStack(
BinaryTreeNode<T> root) {
Stack<BinaryTreeNode<T>> s = new Stack<BinaryTreeNode<T>>();
BinaryTreeNode<T> current = root;
while (current != null) {
s.add(current);
current = current.left;
}
while (!s.isEmpty() && current == null) {
current = s.pop();
out.print(current.data+ " ");
current = current.right;
while (current != null) {
s.add(current);
current = current.left;
}
}
}
Let us consider the below tree for example
1
/ \
2 3
/ \
4 5
Step 1 Creates an empty stack: S = NULL
Step 2 sets current as address of root: current -> 1
Step 3 Pushes the current node and set current = current->left until current is NULL
current -> 1
push 1: Stack S -> 1
current -> 2
push 2: Stack S -> 2, 1
current -> 4
push 4: Stack S -> 4, 2, 1
current = NULL
Step 4 pops from S
a) Pop 4: Stack S -> 2, 1
b) print "4"
c) current = NULL /*right of 4 */ and go to step 3
Since current is NULL step 3 doesn't do anything.
Step 4 pops again.
a) Pop 2: Stack S -> 1
b) print "2"
c) current -> 5/*right of 2 */ and go to step 3
Step 3 pushes 5 to stack and makes current NULL
Stack S -> 5, 1
current = NULL
Step 4 pops from S
a) Pop 5: Stack S -> 1
b) print "5"
c) current = NULL /*right of 5 */ and go to step 3
Since current is NULL step 3 doesn't do anything
Step 4 pops again.
a) Pop 1: Stack S -> NULL
b) print "1"
c) current -> 3 /*right of 5 */
Step 3 pushes 3 to stack and makes current NULL
Stack S -> 3
current = NULL
Step 4 pops from S
a) Pop 3: Stack S -> NULL
b) print "3"
c) current = NULL /*right of 3 */
Now what if we can't use extra space. Then, we use Morris traversal.
Method 3 - Using Morris traversal
For BST traversal, recursion is a natural way of thought. But
sometimes interviewer want to know the iterative way of traversal.
Inorder traversal without recursion:
Using Morris Traversal, we can traverse the tree without using stack and recursion. The idea of Morris Traversal is based on
Threaded Binary Tree.
In this traversal, we first create links to Inorder successor and print
the data using these links, and finally revert the changes to restore
original tree.
1. Initialize current as root
2. While current is not NULL
If current does not have left child
a) Print current’s data
b) Go to the right, i.e., current = current->right
Else
a) Make current as right child of the rightmost node in current's left subtree
b) Go to this left child, i.e., current = current->left
Using Morris Traversal, we can traverse the tree without using stack and recursion. The idea of Morris Traversal is based on
Threaded Binary Tree.
In this traversal, we first create links to Inorder successor and print
the data using these links, and finally revert the changes to restore
original tree.
1. Initialize current as root
2. While current is not NULL
If current does not have left child
a) Print current’s data
b) Go to the right, i.e., current = current->right
Else
a) Make current as right child of the rightmost node in current's
left subtree
b) Go to this left child, i.e., current = current->left
Here is the code in java
//MorrisTraversal
public static <T> void InorderTraversalIterativeWithoutStack(
BinaryTreeNode<T> root) {
BinaryTreeNode<T> current, pre;
if (root == null)
return;
current = root;
while (current != null) {
if (current.left == null) {
System.out.print(current.data + " ");
current = current.right;
} else {
pre = current.left;
while (pre.right != null && pre.right != current)
pre = pre.right;
if (pre.right == null) {
pre.right = current;
current = current.left;
} else {
pre.right = null;
System.out.print(current.data + " ");
current = current.right;
}
}
}
}
Here is the tree after this algo(taken from
http://articles.leetcode.com/2010/04/binary-search-tree-in-order-traversal.html):
Comparison between Method 2 and 3
Compared
to stack based traversal this takes no extra space. Though tree is
modified during traversal, it is reverted back to original.
References
http://leetcode.com/2010/04/binary-search-tree-in-order-traversal.html
http://www.geeksforgeeks.org/inorder-tree-traversal-without-recursion/