Converting an Infix Expression to Postfix expression using a stack

Pre-requisite - What is infix, postfix and prefix?

Infix, Postfix and Prefix notations are three different but equivalent ways of writing expressions. 
Postfix is also known as Reverse Polish Notation or RPN , and prefix expression is also known as Polish notation.

Infix - Operators are written in-between their operands. eg.  A+B
Postfix -  Operators are written after their operands.      eg.  AB+    
Prefix - Operators are written before their operands.      eg.  +AB


Here are more examples:

Infix	Postfix	Prefix	Notes
A * B + C / D	A B * C D / +	+ * A B / C D	multiply A and B, divide C by D, add the results
A * (B + C) / D	A B C + * D /	/ * A + B C D	add B and C, multiply by A, divide by D
A * (B + C / D)	A B C D / + *	* A + B / C D	divide C by D, add B, multiply by A

Example taken from http://www.cs.man.ac.uk/~pjj/cs212/fix.html.

Converting infix to postfix expression

Converting and infix expression to postfix or Reverse Polish notation.
I have used a stack ADT developed using a linked list. I prefer linked lists as memory can be allocated dynamically.
One famous algorithm is the Shunting yard algorithm. The approach used in this article is the usual input and stack precedence comparison algorithm.
Precedence values of stack and input characters

Symbols Input Precedence Stack precedence

+,-          1                 2
*,/          3                 4
$,^          6                 5
operands     7                 8
(            9                 0
)            0                 -
#            -                 -1

Pseduocode
To do so, we have to add the operator to the stack, and operands to the string expression, and whenever we find a lower priority operator, we pop out the operator with higher precedence and append to the expression. When whole string expression finishes, we get the postfix expression.

There is an algorithm to convert an infix expression into a postfix expression. It uses a stack; but in this case, the stack is used to hold operators rather than numbers. The purpose of the stack is to reverse the order of the operators in the expression. It also serves as a storage structure, since no operator can be printed until both of its operands have appeared.

Examples of Pseudocode

Example 1 -  A * B + C
Lets take a simple example - A * B + C , which should evaluate to A B * C  +

	current symbol	operator stack	postfix string
1	A		A
2	*	*	A
3	B	*	A B
4	+	+	A B * {pop and print the '*' before pushing the '+'}
5	C	+	A B * C
6			A B * C +

Example 2 - A + B * C
A + B * C becomes A B C * +
>

	current symbol	operator stack	postfix string
1	A		A
2	+	+	A
3	B	+	A B
4	*	+ *	A B
5	C	+ *	A B C
6			A B C * +

Above examples were taken from http://csis.pace.edu/~wolf/CS122/infix-postfix.htm.
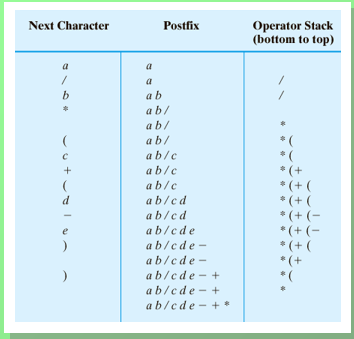
Example 3 - a/b*(c+(d-e))
Consider the following expression -a/b*(c+(d-e))

Suppose a=2, b = 4

Now we do further

Once the conversion, we can evaluate the expression using the stack again.


Implementation in java
Here is java program of the above:

import java.io.*;

class InfPos
{
    private Stack stackADT;
    private String input;
    private String output = "";
    public InfPos(String in)
    {
        input = in;
        stackADT = new Stack();
    }
    public String convert()
    {
        stackADT.push('#');
        System.out.print(stackADT.Peek().item);
         
        for(int j=0; j inpPrec(ch))
            {
                output = output + stackADT.pop().item;
                symbol = stackADT.Peek().item;
            }
            if(stackPrec(symbol) != inpPrec(ch))
                stackADT.push(ch);
            else
                stackADT.pop();
        }
                 
      
        while( !stackADT.isEmpty() )
        {
            if(stackADT.pop().item != '#')
                output = output + stackADT.pop().item;
        }
        return output;
    }
    public int stackPrec(char ch)
    {
        switch(ch)
        {  
            case '+':
            case '-': return 2;
            case '*':
            case '/': return 4;
            case '^':
            case '$': return 5;
            case '(': return 0;
            case '#': return -1;
            default: return 8;
        }
    }
    public int inpPrec(char ch)
    {
        switch(ch)
        {
            case '+':
            case '-': return 1;
            case '*':
            case '/': return 3;
            case '^':
            case '$': return 6;
            case '(': return 9;
            case ')': return 0;
            default: return 7;
        }
    }
 
}
class InfixToPostfix
{
    public static void main(String[] args) throws IOException
    {
        String input, output;
        while(true)
        {
            System.out.print("Enter infix: ");
            System.out.flush();
            InputStreamReader isr = new InputStreamReader(System.in);
            BufferedReader br = new BufferedReader(isr);
            input = br.readLine();
            if( input.equals("") )
                break;
            InfPos theTrans = new InfPos(input);
            output = theTrans.convert();
            System.out.println("Postfix: " + output + '\n');
        }
    }
 
} 

Source